Rangkuman Materi Inti Atom di Tinjau dari Fisika Modern
Ernest Rutherford disebut “Bapak dari Nucleus”. Dia bertujuan untuk menjelasakan struktur dari atom. Sekitar tahun 1900, Marrie and Currie menemukan emisi radio aktivitas dari atom yang disebut α (alpha), β (beta), ϒ (gama). Radiasi alpha adalah peluruhan , ini hanya bisa dihentikan dalam teori. Sinar beta lebih peluruhan, dapat melewati tubuh manusia. Rutherford dalam beberapa percobaannya membuktikan bahwa partikel alpha sama dengan nucleus dari helium atom.
1. Penemuan Nukleus
Walaupun Rutherford menjelaskan stuktur dari nuklues yang massiv di pertengahan 1991, tapi hal ini tak dapat diketahui oleh ilmuwan sampai 1932 bahwa patikel mempunyai komposisi nucleus. Pada pertengahan 1900 nukleus belum diketahui keberadaanya. Walaupun begitu, ada beberapa alsan mengapa electron tidak dapat eksis di antara nucleus.
-
Ukuran Nuklir
-
Nuklir Spin
-
Momen Magnetic Nuklir
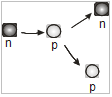
Penemuan dari neutron adalah fenomena yang klasik. Pada tahun 1930, seorang fisikawan jerman, Walther Bothe dan Herbert Becker menggunakan radioaktif dari polonium dengan mengemisikan partikel alpha. Mereka menemukan ketika partikel alpha memborbardir berrilium, sangat memeluruh radioaktif yang diproduksi. Irene Currie dan Freideric Joliot pada tahun 1932 menyatakan bahawa radiasi dapat memeluruh beberapa sentimeter. Radiasi ini tidak mungkin partikel- patikel yang bermuatan, karena partikel bermuatan tersedia energi dan tak bisa memeluruh dalam jarak yang dekat dapat dicapai.ini dapat di asumsikan bahwa radiasi electromagnet (proton) dapat di produksi dari partikel alpha berrilium yang diserang. Photon-photon dikenal dengan sinar gamma ketika mereka mempunyai asal nuklir. Sinar gamma di prouksi di dalam nucleus yang mempunyai energy-energi dan Mev.
Currie dan joliot melakukan beberapa pekerjaan untuk memelajari efek-efek dari peluruhan-peluruhan radiasi baru (yang di produksi oleh α + Be) dalam berbagai macam material. Ketika radiasi menembus paraffin, mereka menemukan bahwa protondengan energi sampai 5.7 Mev yang terlepas. Diasumsikan radiasi sinar gama seperti Compton scattered proses.
Pada tahun 1932, James Chadwick berusaha untuk menjelaskan bahwa radiasi baru dari α + Be yang terdiri dari neutron-neutron, dengan hipotesis elektik partikel netraldengan massa dari proton. Sebuah neutron dapat menembus materiall dengan mudah karenamuatan netral dan mempunyai interaksi dengan momen magnetiknya. Tenaga nuklir sangatlah pendek dan mempunyai mev hanya mungkin 10^-6 interaksi probabilitas dengan nucleus. Chadwick dengan tepat meringkas bahwa jika neutron-neutron sekitar 5.7 Mev dari energy kinetic yang telah diproduksi dalam α + Be reaksi, neutron-neutron dapat secara elastic dengan proton dalam paraffin,daeri perhitungan untuk 5.7 Mev proton-proton. Dalam hasil publikasinya digunakan hasil percobaan untuk mengetahui massa neutron yang berkisar 1.005 u dan 1.008 u, tak jauh dari harga modern 1.0007 u. untuk data-dat eksperimen dan teoritis menunjukan chaddwick menunjukan kehadiran dari neutron.
2. Nuclear properties
Primer konstituen dari nukei yang terdiri dari massa-massa dari proton dan neutron. Formula paling sederhana yaitu atom Hidrogen. Walaupun demikian kita mengetahui bahwa ada penyusun-penyusun hydrogen yang ada. Deutrerium terkadang disebut hydrogen paling berat, mempunyai neutron seperti proton di nucleus. Isotop lainnya yaitu disebut tritium, yang mempunyai satu proton dan dua neutron. Symbol dari nuklues atomic:
$latex ^A_Z X _N $
Dimana Z : no atom
N: no neutron
A: no massa
X: symbol elemen kimia
Setiap spesies nuklir yang terdiri dari Z dan A disebut nuclide. A= N+Z. Nuklida yang mempunyai no. neutron yang sama disebut isoton. Sedangkan, nuklida yang mempunyai harga A yang sama di sebut isobar.
Massa atom didapatkan dari massa unit atomic, yang mendonasi sebagai symbol u. Massa atomic ditemukan pada massa isotop 12c yang mssa atom nya tepat 12 u.
1 u = 1,66054 x 10^-27 kg = 931,49 Mev/C2
Berat dan Ukuran Nuclei
Asumsikan bahwa nuclei terpisah dalam radius R . Partikel-partikel, seperti elektron, proton, neutron, dan alpha, terhambur ketika diproyeksikan meuju nucleus. Hal ini tidak cepat ditemukan ketika interaksi jarak maksimum dalam collision mengacu kepada ukuran nuklir (radius material), atau gaya nuklir menunjukan material nuklir (gaya radial). Electron tidak merespon gaya nuklir akan tetapi dihamburkan dari medan electromagnetic dari nuklues. Penghamburan elekrton menunjukan muatan radial.
Gaya nuklir anatara nucleon paling kuat dari tiga gaya yang diketahui (nuklir, gravitasi, dan electroweak) pada jarak yang dekat. Gaya nuklir sering disebut gaya kuat, dan fisikawan mengunkan dalam kasus nuklir dan gaya kuat muatan dalam. Karena neutron berinteraksi dengan gaya nuklir, penghamburan dari neutron menjabarkan gaya nuklirradial. Banyak penemuan menggunakan partikel yang berbeda, fisikawan menemukan bahwa
Gaya nuklir ≈ massa radial ≈ muatan radial
Radial nuklir dapat didistribusikan sebagai
$latex R = r_0 A^{\frac{1}{s}} $
Dimana r0 ≈ 1,2 x 10^-15 m. Penemuan untuk r0 berkisar 1.0 dan 1,5 x10-15 m. karena nuklir terlalu kecil, kita menggunakan femtometer,dalam skala fm, 1fm = 10-15 m.
Robertt Hofstadter menunjukan presisi pertama dari penemuan penghamburan electondari muatan nklir yang didistribusikan menggunakan energy electron dari 100 ke 500 Mev. Panjang gelombang Debrogli 500 mev electron sekitar 2,5 fm. Penemuan ini dapat menjelaskan untuk semua tapi nuclei yang paling kecil oleh distribusi Fermi kerapatan muatan nuklir:
$latex \rho (r) = \frac{\rho_0}{1+e^{r-R/a}} $
Dimana ρ0 adalah pusat kerapatan n uklir, R adalah jarak dari kerapatan yang diturunkan 50 % dari harga pusat, dan t=4.4 α adalah permukaan tertipis.
Jika kita rumuskan ukuran nuklir, V= (4πR3)/3 atau mengunakan rumus
v = 4/3 . πr03A
Kerapatan dari nuklir dapat di jelaskan dari (Au)/V berkisar 2.3 x 1017 kg/m3 .
Spin Instrinsik
Neutron dan proton mempuntai bilangan kuantum spi yaitu s ≈ ½
Momen instristik magnet
Dengan menganalogikan kepada magneton Bohr, nuklir magnetic adalah
Catatan bahwa menghitung μN adalah massa proton mp , yang membuat magneton nuklir 1800 lebih kecil dari magneton bohr.
3. Deutron
Setelah proton, inti berikutnya yang paling sederhana adalah deuteron, inti 2H. massa deuteron adalah 2.013553 u. dan massa atom deuterium adalah 2.014102 u. perbedaan massa adalah u 2.014102 – 2.013553 u = 0.000549 u , yang hanya massa elektron.
Inti deuteron terikat oleh energi Bd, yang mewakili massa-energi. Lalu, Massa deuteron.
Md = mp + mn – Bd/c2
Eksperimental penentuan Energi ikatan Nuklir kita dapat memeriksa hasil untuk mengikat enegy 2,22-MeV energy ikatan deuteron n dengan menggunakan reaksi nuklir. Kita dapat menghamburkan sinar gamma dari gas deuterium dan mengamati pecahnya deteron menjadi neutron dan proton:h
γ + d → n + p
tipe dari reaksi nuklir ini disebut fotodisintegrasi atau reaksi fotonuklir . persamaan energi minimum yang dibutuhkan untuk untuk potodisintegrasi yaitu
$latex hf_{min} = Bd(1+\frac{Bd}{2M(2H)c2}) $
4. Kekuatan nuklir
Banyak teknik yang digunakan untuk mempelajari kekuatan nuklir. Dalam penghamburan dari proton, deureron kadang – kadang terbentuk dalam reaksi nuklir :
n + p → γ + d
kekuatan nuklir dikatakan jenuh, karena interior nukleon dikelilingi oleh nucleon lainnya dan berinteraksi. Bagaimanapun, nucleon pada permukaan nuklir tidak sepenuhnya terikat, dah kekuatan nuklirnya tidak jenuh. Tentu kita membicarakan secara klasik hal yang seharusnya digambarkan dengan mekanika kuantum.
Kekuatan nuklir diketahui bersifat bergantung pada spin karena keadaan terikat dari deuteron memiliki proton dan netron yang memiliki spin searah, tapi tidak ada keadaan terikat yang memiliki spin berlawanan
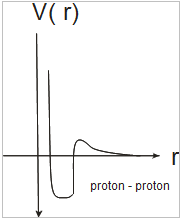
Pembelajaran secara detail dari penghamburan neutron + proton dan proton + proton
Bentuk penggambaran setiap interaksi. Interaksi proton termasuk juga Coloumb effect
5. Kestabilan nuklir
Nucleus dapat dikatakan stabil jika massanya lebih kesil daripada semua kemungkinan kombinasi dari nucleon A.
$latex B = [ M(R) + M(s) – M(^A _Z X)]c^2 $
Energi yang dibutuhkan 1 proton ( atau electron) dari nuklida disebut sebagai energi pemisahan proton ( atau neutron) dan persamaan diatas berguna berguna untuk menemukan energi tersebut
Dalam kekuatan nuklir, jumlah neutron dan proton yang memberikan pengaruh besar, namun gaya coulomb juga harus tetap dipertimbangkan. Energi elektrostatik yang dibutuhkan untuk memuat muatan Ze yang menyebar sepanjang radius R dan bisa di kalkulasikan dengan menentukan kerja yang dibutuhkan untuk membawa muatan kedalam bola, yaitu
ΔEcoul = (3(Ze)2) / 5(4π∈0R)
Dan untuk satu proton,
ΔEcoul = (3e2) / 5(4π∈0R)
Pada tauhn 1930an, Niels Bohr, Carl F. Von Weizsäcker, dan lainnya telah banyak menjelaskan fenomena nuklir dengan menganggap inti sebagai interaksi partikel dalam tetes cairan. Model dari inti ini disebut model tetes cairan.
Dalam energi ikat total, formuka massa semi empiris yaitu,
Untuk membandingkan stabilitas relative dari nuklida yang berbeda, penting untuk mengetahui energi ikatan per nucleon. Dengan mengkalkulasikan setiap energi ikat inti yang diketahui, dan dibagi dengan nomer massanya
Model Nuklir
Fisikawan tidak terlalu mengerti tentang kekuatan nuklir . ada beberapa model yang kurang lebih telah sukses dijelaskan.
Secara umum modelnya dibagi menjadi 2 kategori :
-
Model partikel independen, nucleon bergerah hamper bebas di dalam potensial nuklir standar
-
Model interaksi kuat, nucleon berikatan bersama dengan kuat. Model tetesan cairan dapat dijelaskan dengan model ini
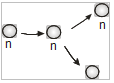
Skema diagram energi proton dan netron untuk beberapa inti antara 12C dan 16O. inti 12C dan 16O cukup stabil, tapi efek dari N≈Z dan pasangan spin penting pada bagian ini
6. Peluruhan Radioaktif
Sebelumnya kita telah mengetahui bahwa nuclei tidak stabil dan bisa meluruh ke sejumlah konfigurasi nucleon A yang mempunyai nomor massa yang lebih rendah. Peluruhan ini dapat terjadi pada emisi dari partikel α, partikel β, partikel γ, proton, neutron, fisi.
Untuk menghitung aktivitas suatu peluruhan kita menggunakan rumus:
Aktivitas = – dN/dt = R, dimana N merupakan jumlah atom yang tidak stabil dari suatu material.
Kita memasukkan tanda negatif disini untuk membuat nilai R positif
Kita melakukan observasi secara eksperimental dari aktivitas dari suatu sampel berhubungan dengan nilai eksponensial berbanding waktu. Jika N(t) adalah jumlah inti radioaktif dalam suatu sampel saat waktu t, dan λ (konstanta peluruhan) adalah probabilitas per satuan waktu dari inti yang meluruh, maka R adalah
R = λN(t)
Jumlah dN dari inti yang meluruh pada saat interval waktu t adalah
dN(t) = – R dt = – λN(t) dt
jika kita mengatur dan mengintegrasi 2 persamaan ini, maka kita mempunyai
ʃdN/N = – ʃ λ dt
ln N = – λt + constant
N(t) = e-λt+constant
Ini adalah hukum peluruhan radioaktif, dan berlaku untuk semua jenis peluruhan.
Untuk setengah waktu paruh ditentukan bahwa
t1/2 = -ln ½ / λ = -ln 2 / λ = 0,693/λ
Waktu rata – rata kehidupan τ dirumuskan menjadi
Τ = 1/λ = t½ / ln 2
7. Peluruhan Alpha, Beta, dan Gamma
Saat inti atom meluruh, semua hukum konservasi harus diobservasi: energi massa, momentum linear, momentum angular, dan muatan elektrik. Untuk semua hukum ini, kita menambahkan 1 hukum lagi dalam peluruhan radioaktif yaitu konservasi nucleons. Konservasi nucleons menyatakan bahwa jumlah bilanga nucleons harus sesuai dengan reaksi nuklir rendah energi atau peluruhan.
Konservasi suatu energi adalah
$latex M(\frac{A}{Z} X) = M_D + M_y + D / c^2 $
Dimana Q adalah energi yang dilepaskan sesuai dengan energi kinetik total dari produk reaksi atau disebut energi disintegrasi
-
Peluruhan Alpha
Untuk peluruhan alpha rumusnya menjadi
(A/Z) X →((A-4)/(Z-2))D + α
Q = [ M((A/Z) X) – M((A-4)/(Z-2))D] – M(4He)]c2
Jika Q > 0. Maka peluruhan alpha dapat terjadi.
-
Peluruhan Beta
Untuk peluruhan beta rumusnya menjadi
(A/Z) X →(A/(Z+1)) D + β- + v
Q = [ M((A/Z) X) – M((A/(Z+1)D)]c2
Penangkapan Elektron
Ada satu kemungkinan terjadinya peluruhan beta yaitu penangkapan elektron
Reaksi umum ditulis
(A/Z) X + e- →(A/(Z-1)) D + v
Q = [ M((A/Z) X) – M((A/(Z-1))D)]c2
-
Peluruhan Gamma
AX*→AX + γ
AX*(E>)→AX*(E<) + γ
8. Inti Nukleotida
Inti yang tidak stabil di alam menunjukkan radioaktifitas alamiah. Inti yang dibuat dari laboratorium merupakan radioaktifitas buatan. Namun, hal ini dapat diketahui waktu luruhnya dengan menggunakan isotop timbal. Isotop ini tidak mempunyai peluruhan dan tidak bersifat radioaktif. Biasanya peluruhan uranium tidak terlalu memakan waktu seperti umur bumi sehingga 235U sudah meluruh menjadi 207Pb. Tetapi untuk 238U waktu luruhnya sangat panjang sehingga belum semuanya meluruh menjadi 206Pb.
Cara kedua untuk mengetahui waktu luruh adalah dengan menggunakan karbon 14.
n + 14N→14C + p
Karbon 14 menjadi karbon 12 didapat secara alami pada molekul CO2
Karbon 14 ini dibandingkan dengan karbon 12 lalu didapat nilai R yang selanjutnya didapat waktu luruhnya. Metode ini dapat digunakan untuk mengetahui waktu paruh fosil, mengetahui umur suatu lapisan tanah di bumi dan sebagainya.




1 comment