Kunci jawaban matematika kelas 10 halaman 68 bab 2 semester 1
Kunci Jawaban Matematika Kelas 10 Semester 1 Kurikulum Merdeka Halaman 68
Berikut ini adalah kunci jawaban dan pembahasan soal Matematika kelas 10 Semester 1 Kurikulum Merdeka halaman 68, yang terkait dengan Uji Kompetensi Bab 2. Soal-soal yang dibahas mencakup berbagai konsep tentang barisan dan deret, termasuk barisan aritmetika dan geometri.
Soal 1: Menentukan Suku ke-10 dan Jumlah 10 Suku Pertama
a. Deret 4 + 2 + 1 + …
Dari deret tersebut, kita dapat mengidentifikasi bahwa ini adalah deret geometri dengan suku pertama $ a = 4 $ dan rasio $ r = \frac{1}{2} $. Untuk menentukan suku ke-10 ($ U_{10} $) dan jumlah 10 suku pertama ($ S_{10} $), kita dapat menggunakan rumus:
$$
U_n = a \cdot r^{n-1}
$$
$$
S_n = a \cdot \frac{1 – r^n}{1 – r}
$$
Dengan substitusi nilai $ a = 4 $ dan $ r = \frac{1}{2} $, maka:
$$
U_{10} = 4 \cdot \left(\frac{1}{2}\right)^9 = \frac{4}{2^9} = \frac{1}{2^7}
$$
$$
S_{10} = 4 \cdot \frac{1 – \left(\frac{1}{2}\right)^{10}}{1 – \frac{1}{2}} = 4 \cdot \frac{1 – \frac{1}{1024}}{\frac{1}{2}} = 4 \cdot 2 \cdot \left(1 – \frac{1}{1024}\right) = 8 \cdot \frac{1023}{1024} = \frac{511}{2^6}
$$
Jadi, suku ke-10 dari deret tersebut adalah $ \frac{1}{2^7} $ dan jumlah 10 suku pertamanya adalah $ \frac{511}{2^6} $.
b. Deret 4 + 1 + (-2) + …
Deret ini merupakan barisan aritmetika dengan suku pertama $ a = 4 $ dan beda $ b = -3 $. Untuk menentukan suku ke-10 ($ U_{10} $) dan jumlah 10 suku pertama ($ S_{10} $):
$$
U_{10} = a + 9b = 4 + 9(-3) = -23
$$
$$
S_{10} = \frac{10}{2} (a + U_{10}) = 5(4 + (-23)) = 5(-19) = -95
$$
Jadi, suku ke-10 dari deret tersebut adalah $ -23 $ dan jumlah 10 suku pertamanya adalah $ -95 $.
Soal 2: Menentukan Suku ke-9 Barisan Aritmetika
Diketahui bahwa jumlah dari suku ke-2, suku ke-5, dan suku ke-20 adalah 54. Dengan menggunakan rumus barisan aritmetika $ U_n = a + (n-1)b $, kita dapat menyelesaikan soal ini sebagai berikut:
$$
U_2 + U_5 + U_{20} = 54
$$
$$
(a + b) + (a + 4b) + (a + 19b) = 54
$$
$$
3a + 24b = 54
$$
$$
a + 8b = 18
$$
Dari persamaan di atas, kita dapat menyimpulkan bahwa:
$$
U_9 = a + 8b = 18
$$
Jadi, suku ke-9 dari barisan aritmetika tersebut adalah $ 18 $.
Soal 3: Panjang Pipa yang Dipotong Menjadi 5 Bagian
Sebuah pipa dipotong menjadi 5 bagian, dan panjang setiap bagian membentuk barisan geometri. Diketahui bahwa potongan pipa terpendek adalah 4 cm dan potongan terpanjang adalah 324 cm. Untuk menentukan panjang pipa semula, kita perlu menghitung jumlah semua bagian.
Dari informasi yang diberikan:
$$
U_1 = 4, \quad U_5 = 324
$$
Kita dapat menggunakan rumus barisan geometri $ U_n = a \cdot r^{n-1} $ untuk menentukan rasio $ r $:
$$
U_5 = a \cdot r^4 = 324
$$
$$
4 \cdot r^4 = 324
$$
$$
r^4 = 81
$$
$$
r = 3
$$
Selanjutnya, kita hitung jumlah 5 suku pertama ($ S_5 $):
$$
S_5 = a \cdot \frac{r^5 – 1}{r – 1} = 4 \cdot \frac{3^5 – 1}{3 – 1} = 4 \cdot \frac{243 – 1}{2} = 4 \cdot \frac{242}{2} = 4 \cdot 121 = 484
$$
Jadi, panjang pipa semula adalah $ 484 $ cm.
Soal 4: Jumlah Kursi dalam Ruang Pertemuan
Pada ruang pertemuan, jumlah kursi pada baris tertentu lebih banyak 2 kursi dari baris sebelumnya. Perbandingan banyak kursi pada baris ke-5 dan baris ke-13 adalah 1 : 2. Baris terakhir terisi 50 kursi. Untuk menentukan total kursi, kita perlu menghitung jumlah seluruh baris.
Diketahui:
$$
b = 2, \quad \frac{U_5}{U_{13}} = \frac{1}{2}, \quad U_n = 50
$$
Dengan substitusi:
$$
U_5 = a + 4b = a + 8, \quad U_{13} = a + 12b = a + 24
$$
$$
\frac{a + 8}{a + 24} = \frac{1}{2}
$$
$$
2(a + 8) = a + 24
$$
$$
2a + 16 = a + 24
$$
$$
a = 8
$$
Untuk menentukan jumlah baris ($ n $):
$$
U_n = a + (n – 1)b = 50
$$
$$
8 + 2(n – 1) = 50
$$
$$
2(n – 1) = 42
$$
$$
n – 1 = 21
$$
$$
n = 22
$$
Total kursi ($ S_n $):
$$
S_{22} = \frac{22}{2} (a + U_n) = 11(8 + 50) = 11 \cdot 58 = 638
$$
Jadi, total kursi dalam ruang pertemuan tersebut adalah $ 638 $ kursi.
Soal 5: Jumlah Deret Geometri Tak Hingga
Diketahui deret geometri tak hingga $ \frac{1}{2} + \frac{1}{xy} + \frac{1}{xy^2} + \ldots $, dengan syarat $ \frac{x + y}{xy} = 1 $. Untuk menentukan jumlah deret tersebut, kita perlu mengidentifikasi rasio $ r $ dan memastikan bahwa deret tersebut konvergen.
Dari informasi $ \frac{x + y}{xy} = 1 $, kita dapat menyimpulkan bahwa $ xy = x + y $. Dengan demikian, rasio $ r $ dari deret tersebut adalah $ \frac{1}{xy} $, dan karena $ xy = x + y $, maka $ r = \frac{1}{x + y} $.
Rumus jumlah deret geometri tak hingga adalah:
$$
S = \frac{a}{1 – r}
$$
Dengan $ a = \frac{1}{2} $ dan $ r = \frac{1}{x + y} $, maka:
$$
S = \frac{\frac{1}{2}}{1 – \frac{1}{x + y}} = \frac{\frac{1}{2}}{\frac{x + y – 1}{x + y}} = \frac{1}{2} \cdot \frac{x + y}{x + y – 1}
$$
- Did a Black Hole Just Explode? Physicists Think So—and It Could Explain Everything - February 19, 2026
- Kunci jawaban matematika kelas 10 halaman 68 bab 2 semester 1 - February 19, 2026
- Dari penggunaan alat hingga perang — inilah 5 cara Jane Goodall merevolusi pemahaman kita tentang kera pithan - February 19, 2026
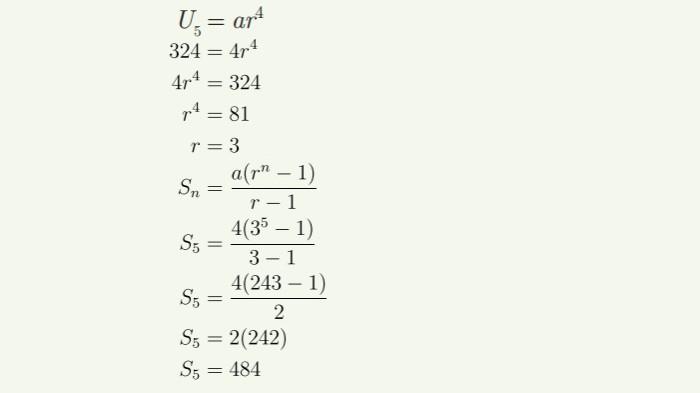
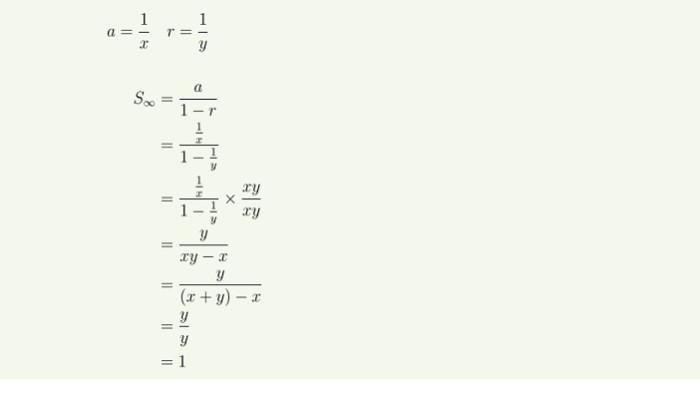
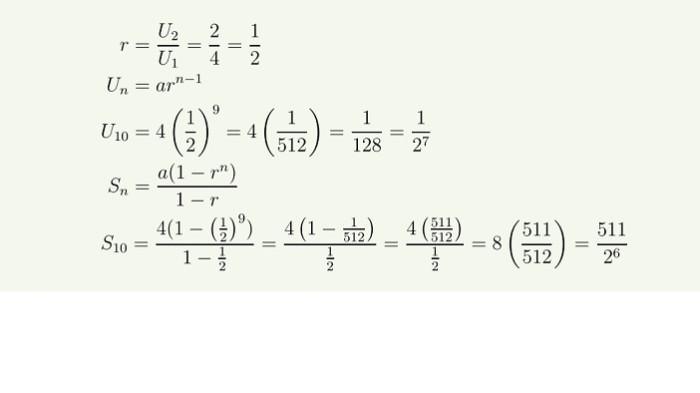
Leave a Reply